Motivation

Das Mach-Zehnder-Interferometer wird oftmals genutzt, um die grundlegenden Ideen der Quantenphysik an einem System zu erläutern, das auch für den Schulunterricht geeignet ist.

In den neuen Bildungsstandards für das Fach Physik werden folgende grundlegenden Begriffe für beide Anforderungsniveaus genannt:

• Stochastische Vorhersagbarkeit,
•  Interferenz und Superposition,
• Determiniertheit der Zufallsverteilung,
• Komplementarität
• Zusammenhänge der Größen Energie, Impuls, Frequenz und Wellenlänge zur Beschreibung von Quantenobjekten
• Realität, Lokalität, Kausalität und Determinismus

Für das grundlegende Anforderungsniveau soll Interferenz am Doppelspalt als grundlegendes Experiment betrachtet werden, auf erhöhrem Niveau kommt das Interferometer dazu. Im neuen niedersächsichen KC Physik Sek II wird darüber hinaus für das erhöhte Niveau speziell das Mach-Zehnder-Interferometer genannt. Deshalb wurden dazu von der NUN-Gruppe Physik Fortbildungsmaterialien erstellt, welche hier - soweit sie das Mach-Zehnder-Interferometer betreffen - mit ergänzenden Bemerkungen dargestellt werden.

Zur Verfügung gestellte Materialien

Alle Dateien werden in einem gesonderten Bereich zum Download angeboten. Dazu gehören u.a. 

• Unterrichtsgang - Vorschlag nach neuem KC Niedersachen (Power-Point-Präsentation)
• Begriffe - Glossar (pdf)
• Erläuterung am Mach-Zehnder-Interferometer (pdf)
• Interferometer "Baukasten" (für Aufgaben und Vorlage für Laser-Cutter)
• Anmerkungen zur "Welcher-Weg-Information" im Quantenradierer

Alle Materialien unterliegen Urheberrechten und Lizenzen, die beachtet werden müssen, zumeist sind sie freigegeben unter 
CC BY -NC-SA Namensnennung-nicht kommerzielle-Weitergabe unter gleichen Bedingungen
Diese erlaubt in der Regel die kostenlose Verwendung im Unterricht.

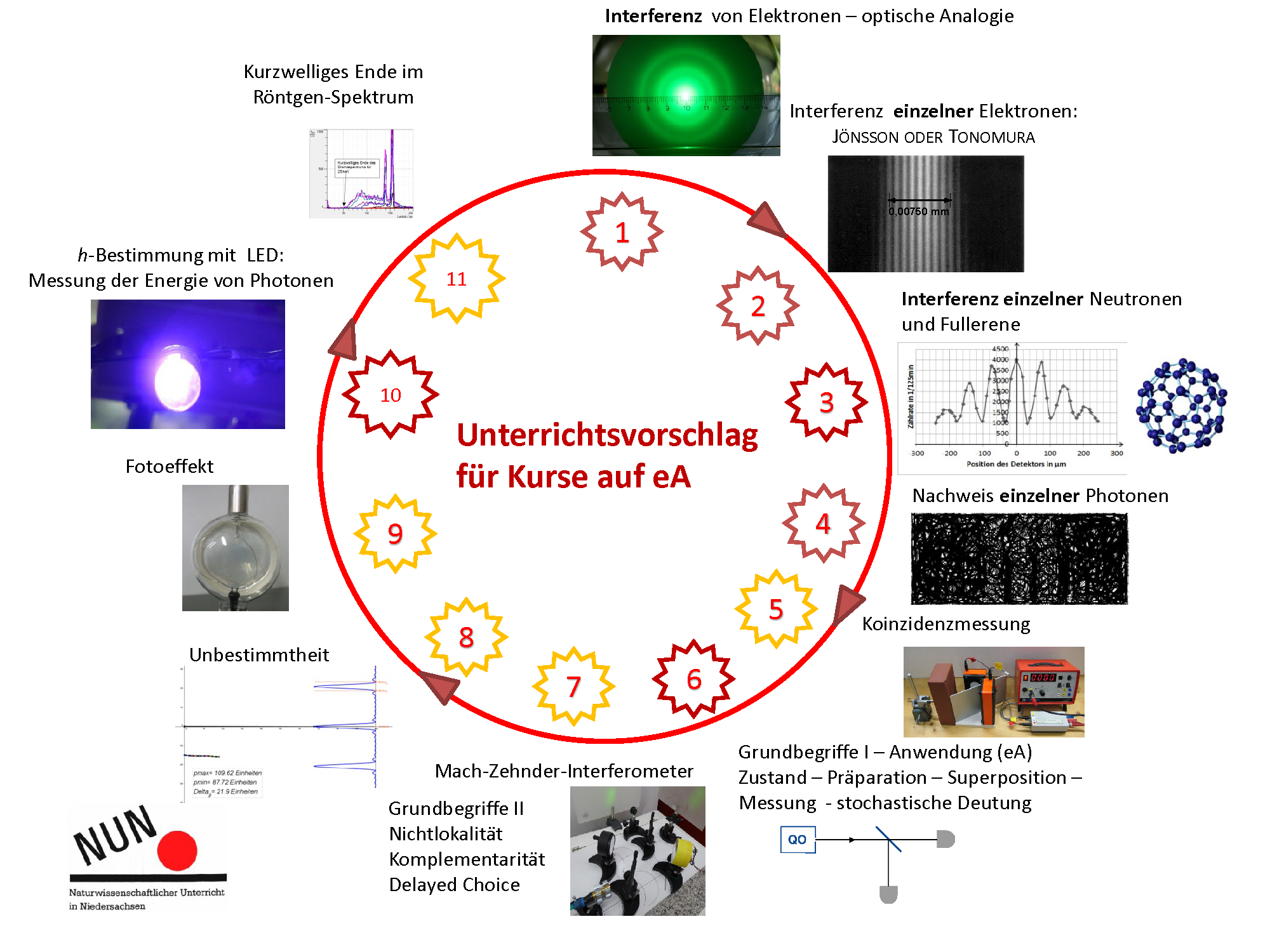
Vorschlag für einen Unterrichtsgang Quantenphysik (eA und gA)

zur Präsentation

Interferometer "Baukasten"

Im Interferometer-Baukasten können Diagramme von Interferometern, beispielsweise für Arbeitsblätter,  erstellt werden.

Interferometer-Bauskasten

aus Sperrholz 

In den Materialien finden sich auch Dateien, um den digitalen Interferometer-Baukasten mit einem Lasercutter aus 3mm Sperrholz zu schneiden.  

Zustand (Wellenfunktion)

Präparation  (eines Zustands)

Superposition  (Überlagerung)

Messung von Größen

Stochastische Deutung - Determinismus

komplementäre Größen

Polarisation

Interferenz

Interferenz

Komplementarität

Delayed Choice

Kausalität

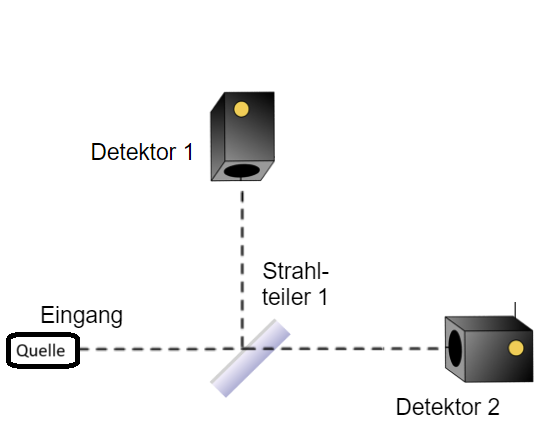
1. Quelle mit einem Strahlteiler und zwei Detektoren

Am „Eingang“ befindet sich eine Quelle für Quantenobjekte, beispielsweise Photonen, deren Eigenschaften, bei einem Laser z.B. Wellenlänge und Polarisationsrichtung bekannt sind. Damit ist der Zustand der Quantenobjekte bekannt, das Herstellen eines solchen Zustands als Ausgangspunkt eines Experiments nennt man Präparation des Zustands.  

Quelle:  Screenshot QuVis-Simulation (bearbeitet)

Die Ausbreitung des Zustands durch den Apparat kann vollständig analog zur Ausbreitung von Wellen beschrieben werden. Trifft der Zustand auf den Strahlteiler, so wird er durch Wechselwirkung mit dem Strahlteiler in zwei Teilzustände aufgeteilt, einen gerade durchgelassenen (transmittierten) Anteil, und einen reflektierten Anteil, der gegenüber dem transmittierten Anteil um eine Phase von   verschoben ist. Hinter dem Strahlteiler besteht der Zustand also aus zwei Teilzuständen, die sich zu dem Zustand additiv (also ungestört) überlagern. Diese additive Überlagerung bezeichnet man als Superposition. Trifft der Zustand dann auf die beiden Detektoren, spricht aber bei jedem einzelnen Quantenobjekt nur ein Detektor an: es gibt keine Koinzidenz. Diese Messung hat als mögliche Ergebnisse für jeden Detektor nur die Messwerte 0 (nicht detektiert) oder 1 (detektiert) und beide Werte sind verschieden. Welcher Messwert eintritt, ist zufällig, die Wahrscheinlichkeit dafür berechnet man aus dem Betragsquadrat der Amplituden der Teilzustände. Wird der Strahl hälftig aufgeteilt, ist diese Wahrscheinlichkeit für jeden Detektor jeweils 1/2. (Andere Verhältnisse sind möglich.)
Zwar wurde der Zustand, der alle Informationen über das Quantenobjekt enthält, in eine Superposition von zwei Teilzuständen aufgeteilt, aber nicht das Quantenobjekt selbst, das nur an einem Ort der Messapparatur nachgewiesen werden kann. Dass man nicht annehmen darf, dass ein Quantenobjekt sich für einen der beiden Teilzustände entscheidet, also der andere Teilzustand dann im Weiteren keine Rolle mehr spielt, wird durch das Interferenzexperiment in Abschnitt 3. gezeigt.

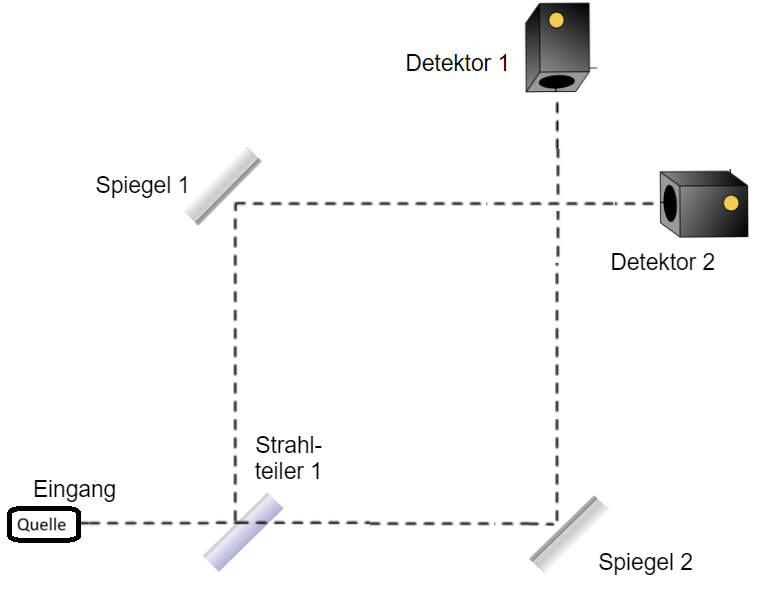
2. Quelle mit Strahlteiler, zwei Spiegeln und zwei Detektoren

Quelle:  Screenshot QuVis-Simulation(bearbeitet)

Zunächst werden noch zwei Spiegel eingebaut. Der Zustand wechselwirkt mit den Spiegeln, aber jeweils nur mit dem Teilzustand am Ort des Spiegels. Ein Spiegel bewirkt eine Richtungsänderung und eine Phasenverschiebung um   von beiden Teilzuständen. Die Messung mit den beiden Detektoren liefert dasselbe Ergebnis wie vorher: Ein Quantenobjekt wird an jedem der Detektoren mit einer Wahrscheinlichkeit von 1/2 gemessen, da sich die Teilzustände zwar räumlich kreuzen, aber nicht miteinander wechselwirken.

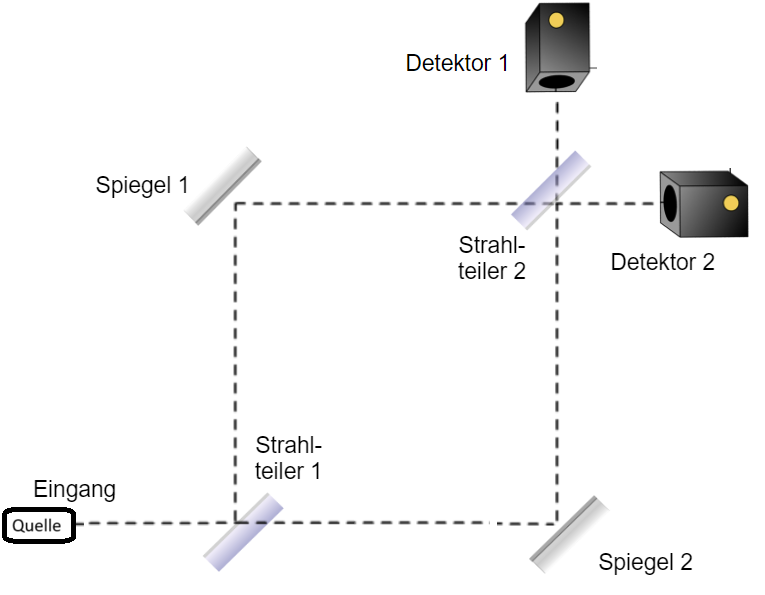
3. Quelle mit zwei Strahlteilern, zwei Spiegeln und zwei Detektoren: Das Mach-Zehnder-Interferometer

Wird der Aufbau um einen weiteren Strahlteiler am Kreuzungspunkt der beiden Teilzustände ergänzt, so erhält man ein Mach-Zehnder-Interferometer. An diesem zweiten Strahlteiler findet nun eine weitere Wechselwirkung mit dem Zustand statt. Jeder Teilzustand wird jeweils wieder zum Teil reflektiert und zum Teil transmittiert, der reflektierte Teil jeweils wieder um eine Phase von   verschoben. Hinter dem zweiten Strahlteiler gibt es nun eine neue Superposition: 

Quelle:  Screenshot QuVis-Simulation

Auf den Detektor 1 trifft die Superposition aus zwei der vier Teilzustände: der, der an beiden Strahlteilern transmittiert wurde und der, der an beiden Strahlteilern reflektiert wurden. Da die Phasen gegeneinander nun um   verschoben sind, kommt es zur destruktiven Interferenz. 
Auf den Detektor 2 trifft die Superposition aus den anderen zwei der vier Teilzustände: der, der am ersten Strahlteilern transmittiert und am zweiten Strahlteiler reflektiert wurde und der, der am ersten Strahlteiler reflektiert und am zweiten Strahlteilern transmittiert wurde. Da die Phasen gegeneinander nicht verschoben sind, kommt es zur konstruktiven Interferenz. 
Dies bedeutet, dass der Detektor 2 alle Quantenobjekte mit Wahrscheinlichkeit 1 registriert, der Detektor 1 mit Wahrscheinlichkeit 0, also nichts registriert. Dies gilt aber nur für die optische Achse des Interferometers, wo die Weglängen gleich sind. Abseits der optischen Achse kommen je nach Ort des Detektors Gangunterschiede hinzu, sodass es auf einem Schirm zu einem Interferenzmuster kommt.
Die Interferenz zeigt, dass die Superposition der Teilzustände entscheidend für das Ergebnis verantwortlich ist. Zur Vorhersage des Messergebnisses trägt also immer die Information des gesamten Systems bei, auch wenn die Teilzustände räumlich getrennte Bereiche durchlaufen: Dies bezeichnet man mit dem Begriff Nichtlokalität. 
Dies zeigt auch, dass die Aufteilung der (Teil-)Zustände an den beiden Strahlteilern nicht als zweistufiges Zufallsexperiment beschrieben werden darf, sondern der Zufall erst bei der Messung ins Spiel kommt. Die zugehörigen Wahrscheinlichkeiten berechnen sich nämlich aus dem Betragsquadrat der Amplitude der Summe von Teilzuständen, welche bei Interferenz von der Summe der Betragsquadrate der Amplituden der Teilzustände verschieden ist. Man muss also immer erst den Zustand des Systems bis zur Messapparatur berechnen (diese Berechnung beinhaltet keinen Zufall), erst danach die Wahrscheinlichkeiten für die Messergebnisse. Dies ist die sogenannte stochastische Deutung der Quantenphysik.

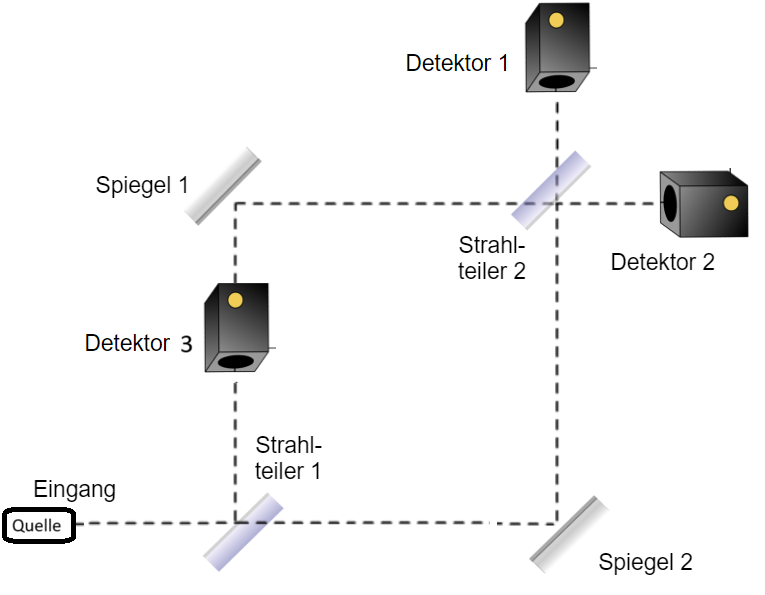
4. Komplementarität am Mach-Zehnder-Interferometer

Es stellt sich die Frage, ob man zusätzlich zur Messung eines Quantenobjekts am Ausgang des Interferometers herausfinden kann, durch welchen Arm des Interferometers es dorthin gelangt ist. 

Quelle:  Screenshot QuVis-Simulation (bearbeitet)

Dazu könnte man beispielsweise einen dritten Detektor in einen der Arme stellen. Wird das Quantenobjekt dort gemessen oder nicht, erhält man die erwünschte zusätzliche Information. Allerdings ist dann hinter dem Detektor kein Teilzustand mehr vorhanden, welcher hinter dem zweiten Strahlteiler zur Interferenz führen könnte, diese ist nicht mehr beobachtbar. Dies bezeichnet man als Komplementarität: Entweder man erhält die Information über den Ort eines Quantenobjekt oder es kommt zur Interferenz, beides ist nicht gleichzeitig möglich. Aufwändigere Experimente, die den Teilzustand nicht löschen, sondern durch eine weitere Wechselwirkung „markieren“, kommen zu demselben Ergebnis.

5. Delayed-Choice Experimente mit dem Mach-Zehnder-Interferometer

Die Komplementarität für sich beantwortet noch nicht die Frage, ob sich ein Quantenobjekt in Kenntnis des Versuchsaufbaus, nämlich des Vorhandenseins eines dritten Detektors, am Strahlteiler für einen der Teilzustände entscheidet (wie im Teilchenmodell), oder andernfalls nicht (wie im Wellenmodell).
Bei sogenannten Delayed-Choice (nachträgliche Entscheidung) Experimenten verändert man den Aufbau zu einem Zeitpunkt, nachdem das Quantenobjekt den ersten Strahlteiler bereits passiert hat. Beispielsweise fügt man den zweiten Strahlteiler erst ein, nachdem das Quantenobjekt den ersten Strahlteiler passiert hat. Würde man annehmen, dass es sich ohne dem zweiten Strahlteiler im Aufbau am Strahlteiler für einen Teilzustand entschieden hätte (wie im Teilchenmodell mit einem bestimmbaren Weg), mit dem zweiten Strahlteiler aber nicht (wie im Wellenmodell mit einer Überlagerung von Teilwellen), so würde man schließen, dass es sich beim nachträglichen Einbau auch nachträglich noch umentscheiden müsste (delayed choice). Diese Entscheidung müsste aber rückwirkend in der Vergangenheit fallen. Dies widerspricht aber der Tatsache, dass alle Gleichungen der Physik kausal sind. Kausalität bedeutet, dass eine Ursache (hier der Einbau des Detektors) nur solche Wirkungen auf das System haben kann, die in der Zukunft liegen, nie in der Vergangenheit, und auch nur an solchen Orten, die mit höchstens Lichtgeschwindigkeit erreichbar sind (gemäß der speziellen Relativitätstheorie von Albert Einstein). 
Diese Überlegungen zeigen, dass sich ein Quantenobjekt nie für einen Teilzustand einer Superposition entscheidet, weder zu einem Zeitpunkt noch rückwärts in der Vergangenheit, sondern immer alle Informationen aus allen Teilzuständen zum Messergebnis beitragen, auch wenn diese vorher gleichzeitig durch verschiedene, räumlich getrennte Bereiche gelaufen sind. Genau das wird im Experiment beobachtet.
Dies widerspricht unserer klassischen Denkweise, nach der sich ein Objekt nur an einem Ort befinden kann und zu einer Zeit immer nur an seinem Ort mit anderen Objekten wechselwirken kann. Ein Zustand, der aus entsprechenden Teilzuständen bestehen, kann aber an räumlich getrennten Orten gleichzeitig wechselwirken, und alle Auswirkungen dieser Wechselwirkungen, beschrieben durch die Superposition aller Teilzustände am Ort des Detektors, bestimmen das – dann aber zufällige – Messergebnis, was unserer Vorstellung widerspricht. Es zeigt auch, dass die Vorstellung „Welle oder Teilchen“ nicht zur Erklärung taugt – das Quantenmodell ist ein neues Modell, das zwar Aspekte von Wellen- und Teilchenmodell übernimmt (in der Theorie vom Wellenmodell die räumlich ausgedehnten Zustände, im Experiment die Messung von Einzelereignissen), aber wesentliche neue Aspekte beinhaltet, die im Konflikt zu den bisherigen Vorstellungen stehen.

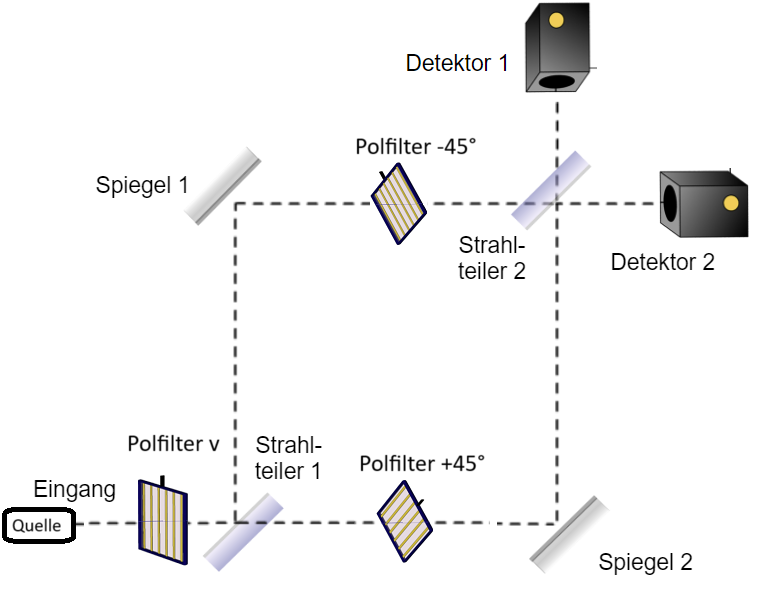
6. Verwendung von Polarisationsfiltern

Erzeugt ein Laser unpolarisiertes Licht, so kann man den Zustand nicht genau angeben, deshalb verwendet man für die Präparation des Zustands eine Quelle mit bekannter Polarisation, z.B. vertikal (v).

Quelle:  Screenshot QuVis-Simulation (bearbeitet)

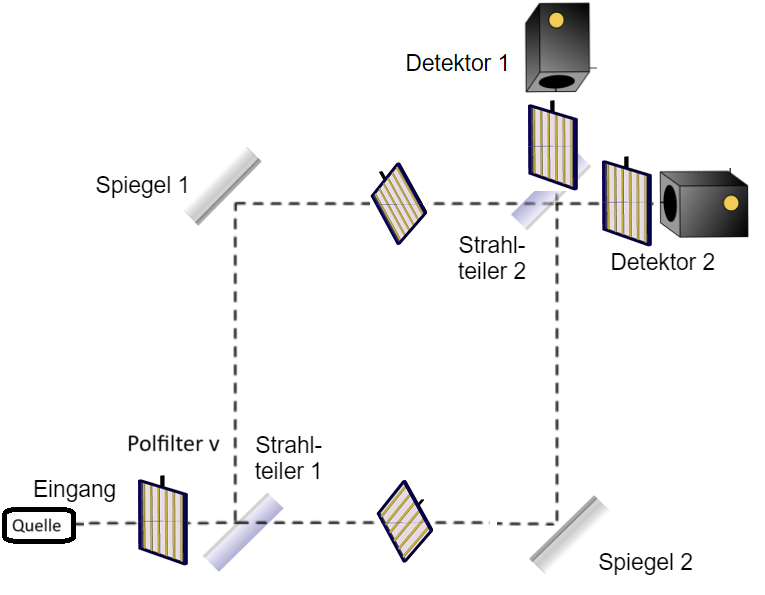
Stellt man nun in die zwei Arme des Interferometers zwei weitere Polfilter mit +45° und -45° Richtungen, die senkrecht zueinander stehen, so bewirkt der Strahlteiler 2 im Ausgang eine Superposition von zwei Teilzuständen, die jeweils wiederum aus zwei senkrecht zueinander stehenden Teilen bestehen. Am Detektor 2  überlagern sich +45° und -45° zu 0° (vertikal), da es keine Phasenverschiebung gibt. Am Detektor 1   ist der -45°-Zustand aufgrund der Phasenverschiebung um    auf +135° gedreht, sodass sich +45° und +135° zu 90° (horizontal), überlagern. Da zwei senkrecht zueinander stehende Zustände sich vektoriell addieren und in der Superposition sich insbesondere nicht auslöschen können, kommt es nicht mehr zu Interferenz, an beiden Detektoren werden gleich viele Ereignisse gemessen und es ist sind keine Interferenzmuster mehr zu sehen. Allerdings stehen die Polarisationsrichtungen an beiden Detektoren senkrecht aufeinander. Abseits der optischen Achse sind diese je nach Ort auf einem Schirm gedreht.

Quelle:  Screenshot QuVis-Simulation (bearbeitet)

Fügt man nun in beide Ausgänge wieder vertikale Polarisationsfilter ein, so wird jeweils der vertikale Anteil ausgewählt, und die ursprünglichen Interferenzmuster sind wieder sichtbar, da auf der optischen Achse nur bei Detektor 2 etwas ankommt, nichts bei Detektor 1, aber abseits der optischen Achse wieder Anteile, die aufgrund der parallelen Polarisationsrichtungen Interferenz zeigen kann. Eigentlich hat man effektiv nur die Teilzustände durch zwei aufeinander folgende Polarisationsfilter auf 25% ihrer ursprünglichen Amplitude reduziert. 

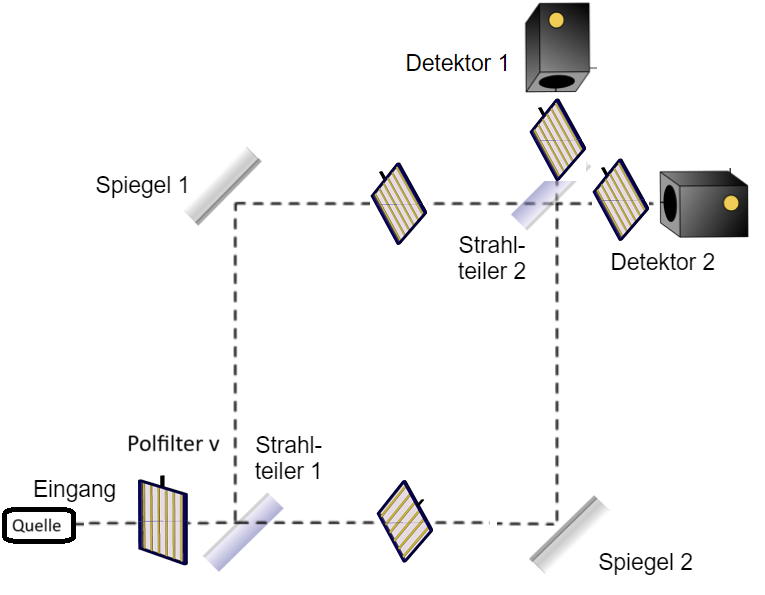
Als zweite Möglichkeit kann man die beiden Polarisationsfilter hinter dem zweiten Strahlteiler auch beide auf z.B. -45° einstellen.  

Quelle:  Screenshot QuVis-Simulation (bearbeitet)

Dann wird aus den beiden Teilzuständen hinter dem zweiten Strahlteiler nur der entsprechende Anteil herausgefiltert. Dessen  Amplitude berechnet stimmt mit aus dem Anteil des entsprechenden Interferometerarms mit -45° Polarisation überein. Oftmals wird nun behauptet, dass man daher weiß, dass die Quantenobjekte auch auf diesem Weg durch das Interferometer gelangt sind, da sie ansonsten nacheinander zwei senkrecht zueinander stehende Polarisationsfilter passiert haben müssten. Diese klassisch gedachte Deutung als „Welcher-Weg-Information“ ist aber nicht gerechtfertigt. Zum einen besagt die stochastische Deutung, dass alle Quantenobjekte in einem Zustand dieselbe Wahrscheinlichkeit besitzen, detektiert zu werden, also alle Photonen im vertikal polarisierten Teilzustand am Detektor 2 mit derselben Wahrscheinlichkeit durch den -45°-Filter gelangen, egal aus welchem Arm sie stammten (wenn man das überhaupt sagen darf, weil „Weg“ keine beobachtbare Größe ist.), weil es gibt keine sogenannten versteckten Variablen gibt, die das Verhalten eines Quantenobjekts zusätzlich bestimmen. Der Zustand der Photonen selbst trägt daher keine Informationen über die Vergangenheit mit sich, die Photonen haben sich nach der Superposition am Strahlteiler nicht ihren Zustand davor gemerkt. Zu anderen gibt es auch den Tunneleffekt, der zeigt, dass Quantenobjekte sich auch auf klassisch verbotenen „Wegen“ „bewegen“ können. Möchte man die Quantenobjekte so „markieren“, dass aus der Messung der „Weg“ (eigentlich nur en Ort) bekannt ist, so muss man eine entsprechende Apparatur in diesem Arm des Interferometers aufstellen, so wie beim Beispiel des Detektors im Abschnitt zur Komplementarität, diese Apparatur erzeugt zum Beispiel zusätzliche Photonen, die man messen kann, aber so, dass das ursprüngliche Photon in einem veränderten Zustand noch zum Strahlteiler gelangen kann. (Man sagt, die Ortsinformation wird mit der Polarisation verschränkt, die Interferenz geht verloren.)  Solche Experimente gibt es.  

Das Ergebnis ist stets dasselbe: Man muss, ausgehend vom präparierten Zustand, den Zustand eines Quantenobjekts zeitlich durch alle möglichen räumlichen Bereiche des Systems verfolgen und alle Wechselwirkungen in diesen Bereichen berücksichtigen, und am Ende, und erst dann, aus diesen Informationen, also dem Endzustand, die Wahrscheinlichkeiten zu den verwendeten Messungen berechnen. Möchte man zusätzliche Informationen erhalten, muss der Aufbau durch geeignete Wechselwirkungen gestaltet werden. Dann kommt es aber zur Komplementarität. 

Dass immer alle Informationen aus allen (kausal – kein Delayed Choice) erreichbaren Bereichen beitragen, auch wenn diese räumlich getrennt sind, also die Nichtlokalität, lässt sich mathematisch widerspruchsfrei, deterministisch, beschreiben, steht aber im Konflikt zu unserer klassischen Vorstellung, dass zu einer Zeit immer nur Wechselwirkungen an einem Ort, nämlich dem aktuellen eines Objekts, beitragen sollte – dieser Konflikt stellt das gedankliche Kernproblem zum Verständnis der Quantenphysik dar. Er kann auch heute nicht als gedanklich gelöst betrachtet werden.